利用莱文斯坦距离计算两个字符串的相似度

前几天有个朋友问了我一个问题，有两个Excel文件，每个文件都包含一列地址，两个文件的地址在实际中都是一一对应的。但是由于各种原因，两列地址存在误差，数据大概如下：

A Excel	B Excel
网商路100号	网商路第100号
网商路100号	网商路100
网商路100100号	网商101000号

现在需要把这些数据匹配起来，但是两个Excel大概各有30-40W的数据，完全匹配的只有不到20%，剩下的不匹配的数据太多了，不可能手工去匹配，有没有什么办法可以让机器处理先找出最相似的？之前没接触过类似问题，第一反应是把字符串拆开对比，根据匹配的字符个数和匹配的顺序去计算相似度，然后根据一个标准找到最相似的，不过想法太随意了，没法实现和验证。去网上查询类似的问题，发现早就有个算法做这个事情了，就是利用莱文斯坦距离算法计算两个字符串的编辑距离。

莱文斯坦距离(Levenshtein distance)是编辑距离的一种，两个字符串之间的莱文斯坦距离是将一个单词更改为另一个单词所需的最少编辑操作次数。莱文斯坦距离允许的编辑操作包括单个字符的替换/插入/删除。

比如将 网商路10a号x 编辑为 网商路第100号 的过程如下：

网商路10a号x 增加 第 -> 网商路第10a号x
网商路第10a号x 替换 a 为 0 -> 网商路第100号x
网商路第100号x 删除 x -> 网商路第100号

经过3次编辑，网商路10a号x 变成了 网商路第100号，因此编辑距离为3。可以看出编辑距离越小，则两个字符串越相似，最小编辑距离为0，那最大编辑距离是多少呢？如果在最优的条件下，应该等于两个字符串的长度之和（m+n），最简单的操作是经过（m+n）步将两个字符串全部删除成空字符串，这样就相等了。

算法的原理很简单，但是要怎么实现就需要一步一步来理解了，莱文斯坦距离允许的操作有三种，替换/插入/删除，如果字符相等，可以选择不操作。我们可以一一列举一下：

不操作

计算 bc 和 abc 之间的距离，在比较最后一个字符“c”的时候，由于“c”相等，我们可以选择不操作，也就是说bc 和 abc的距离等于子字符串b 和 ab的距离。
替换

计算 abc 和 abf 之间的距离，在比较最后一个字符“f”的时候，由于“c”和“f”不相等，最优的操作是替换，只需要1步，也就是说abc 和 abf的距离等于子字符串ab 和 ab的距离加1。
增加/删除

计算 abc 和 ab 之间的距离，在比较最后一个字符“c”的时候，由于“ab”没有第三个字符，最优的操作是“abc”删除一个“c”，或者“ab”增加一个“c”，只需要1步，也就是说abc 和 ab的距离等于子字符串ab 和 ab 的距离加1。

上面的列举可以看出字符串可以拆成子字符串的距离加0或者加1，子字符串可以继续拆分，直到拆成空字符串。对于可以拆成多个子问题的，可以使用动态规划的方式来解决。

将前面的例子 网商路10a号x 跟 网商路第100号 的编辑距离用二维数组来统计，步骤如下：

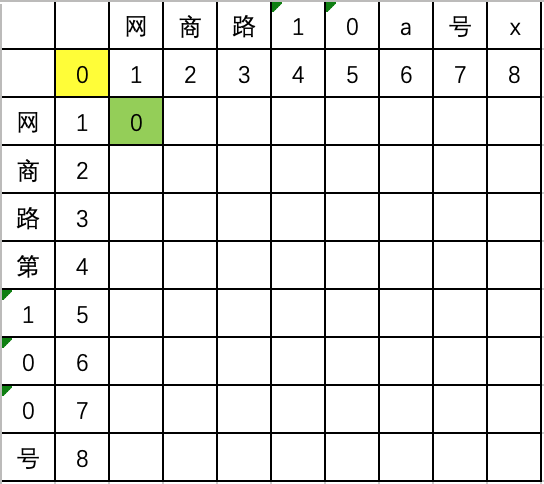
比较第一个字符“网”，由于相等，最优操作是不操作，可以等价于两个空字符串的编辑距离+0，二维数组如下：

黄色为空字符串的编辑距离，绿色为子字符串“网”和“网”的编辑距离
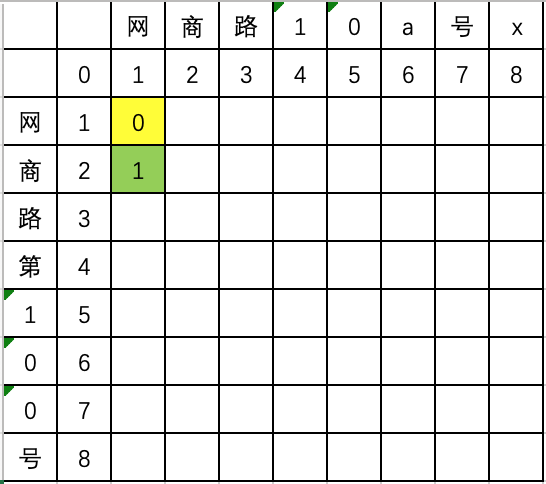
比较“网商”和“网”，最优操作是“网”增加一个“商”，可以等价于两个子字符串“网”的距离+1，二维数组如下：
依次操作下去，最终的最优操作二维数组如下：

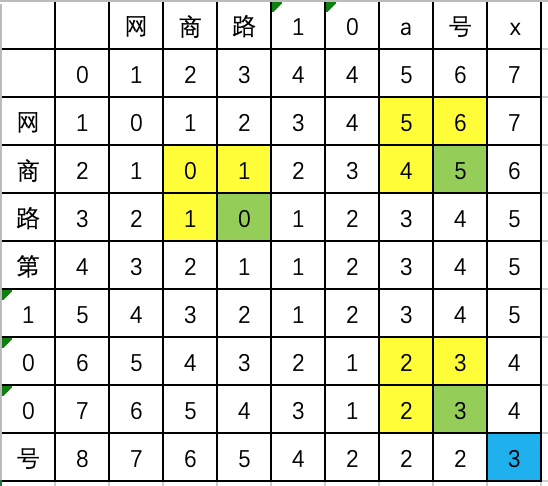
可以发现，计算绿色的格子时，当字符相等时，最优操作是不操作，因此等于左上角的值加0，当字符不相等时，最优操作是替换（左上角加1），增加/删除（左边或上边加1），总结起来就是它的值等于左上三个格子中最小的值加1或加0，最终右下角的值就是整个字符串的最小编辑距离。

整个过程中最重要的是拆分子字符串和最优操作，转成java代码实现如下：

    public class StrCompare {

    public static int compare(String str, String target) {

        int n = str.length();
        int m = target.length();
        int[][] dp = new int[n+1][m+1];

        // 第一个行和第一列设置为空字符串
        for (int i = 0; i < (n + 1) ; i++) {
            dp[i][0] = i;
        }

        for (int i = 0; i < (m + 1) ; i++) {
            dp[0][i] = i;
        }

        // 依次计算各子串的最优操作的编辑距离
        for (int i = 1; i < (n + 1) ; i++) {
            for (int j = 1; j < (m + 1) ; j++) {
                if(str.charAt(i-1) == target.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else {
                    dp[i][j] = Math.min(Math.min(dp[i-1][j-1],dp[i][j-1]),dp[i-1][j]) + 1;
                }
            }
        }

        // 返回最优编辑距离
        return dp[n][m];
    }

}

利用莱文斯坦距离计算两个字符串的相似度

FEATURED TAGS

FRIENDS